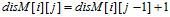最小编辑距离
一 概念
编辑距离(Edit Distance),又称Levenshtein距离,是指两个字串之间,由一个转成另一个所需的编辑操作次数。最小编辑距离,是指所需最小的编辑操作次数。
编辑操作包含:插入、删除和替换三种操作。
二 最小编辑距离解法-动态规划解法
动态规划的核心思想是:将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
由于动态规划解决的问题多数有重叠子问题这个特点,为减少重复计算,对每一个子问题只解一次,我们将其不同阶段的不同状态保存在一个二维数组中。
最小编辑距离算法伪代码:
输入:字符串1-str1 字符串2-str2
输出:最小编辑距离
实质问题:
求解动态规划矩阵。假设我们以str1为主串(即对str1进行操作)
算法:
- 假设str1=ABCD str2=ACD;len1=str1的长度,len2为str2的长度。
- 建立矩阵:
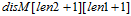
#
A
B
C
D
#
A
C
D
#表示在串前可以插入任何字符。 - 初始化:
#
A
B
C
D
#
0
1
2
3
4
A
1
C
2
D
3
- 三种编辑操作对应着矩阵的三种走法:
| 矩阵方向 | 编辑操作 | 计算公式 |
| 向右走:Right | 删除 |
|
| 向下走:Down | 插入 |
|
| 对角线:Diagonal | 替换|匹配 |
|
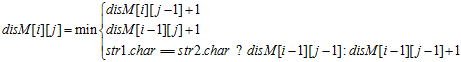
循环计算整个矩阵
| # | A | B | C | D | |
| # | 0 | 1 | 2 | 3 | 4 |
| A | 1 | 0 | 1 | 2 | 3 |
| C | 2 | 1 | 1 | 1 | 2 |
| D | 3 | 2 | 2 | 2 | 1 |
5.  即为最小编辑距离
即为最小编辑距离
三 应用
最小编辑距离通常作为一种相似度计算函数被用于多种实际应用中,详细如下:(特别的,对于中文自然语言处理,一般以词为基本处理单元)
- 生物领域中DNA分析:比较 DNA 序列并尝试找出两个序列的公共部分。如果两个 DNA 序列有类似的公共子序列,那么这些两个序列很可能是同源的。在比对两个序列时,不仅要考虑完全匹配的字符,还要考虑一个序列中的空格或间隙(或者,相反地,要考虑另一个序列中的插入部分)和不匹配,这两个方面都可能意味着突变(mutation)。在序列比对中,需要找到最优的比对(最优比对大致是指要将匹配的数量最大化,将空格和不匹配的数量最小化)。
- NLP中应用:即两个字符串的相似计算函数可用于下面的任务。
- 拼写纠错(Spell Correction):又将每个词与词典中的词条比较,英文单词往往需要做词干提取等规范化处理,如果一个词在词典中不存在,就被认为是一个错误,然后试图提示N个最可能要输入的词——拼写建议。常用的提示单词的算法就是列出词典中与原词具有最小编辑距离的词条。
- 命名实体抽取(Named Entity Extraction):由于实体的命名往往没有规律,如品牌名,且可能存在多种变形、拼写形式,这样导致基于词典完全匹配的命名实体识别方法召回率较低,为此,我们可以使用编辑距离由完全匹配泛化到模糊匹配,先抽取实体名候选词。
- 实体共指(Entity Coreference):通过计算任意两个实体名之间的最小编辑距离判定是否存在共指关系。
- 字符串核函数(String Kernel):最小编辑距离作为字符串之间的相似度计算函数,用作核函数,集成在SVM中使用。